Inheritance diagram for svgfig.Ticks:

Public Member Functions
def	__init__ (self, f, low, high, ticks=-10, miniticks=True, labels=True, logbase=None, arrow_start=None, arrow_end=None, text_attr={}, attr)

def	__repr__ (self)

def	compute_logminiticks (self, base)

def	compute_logticks (self, base, N, format)

def	compute_miniticks (self, original_ticks)

def	compute_ticks (self, N, format)

def	interpret (self)

def	orient_tickmark (self, t, trans=None)

def	regular_miniticks (self, N)

def	SVG (self, trans=None)

Public Attributes
	arrow_end

	arrow_start

	attr

	f

	high

	labels

	last_miniticks

	logbase

	low

	miniticks

	text_attr

	ticks

Static Public Attributes
dictionary	defaults = {"stroke-width":"0.25pt"}

float	minitick_end = 0.75

float	minitick_start = -0.75

int	text_angle = 0

dictionary	text_defaults = {"stroke":"none", "fill":"black", "font-size":5}

float	text_start = 2.5

float	tick_end = 1.5

float	tick_start = -1.5

Detailed Description

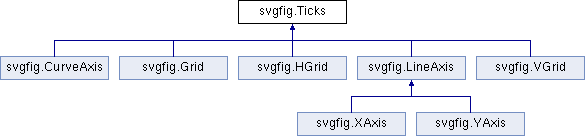
Superclass for all graphics primatives that draw ticks,
miniticks, and tick labels.  This class only draws the ticks.

Ticks(f, low, high, ticks, miniticks, labels, logbase, arrow_start,
      arrow_end, text_attr, attribute=value)

f                       required        parametric function along which ticks
                                        will be drawn; has the same format as
                                        the function used in Curve
low, high               required        range of the independent variable
ticks                   default=-10     request ticks according to the standard
                                        tick specification (see below)
miniticks               default=True    request miniticks according to the
                                        standard minitick specification (below)
labels                  True            request tick labels according to the
                                        standard tick label specification (below)
logbase                 default=None    if a number, the axis is logarithmic with
                                        ticks at the given base (usually 10)
arrow_start             default=None    if a new string identifier, draw an arrow
                                        at the low-end of the axis, referenced by
                                        that identifier; if an SVG marker object,
                                        use that marker
arrow_end               default=None    if a new string identifier, draw an arrow
                                        at the high-end of the axis, referenced by
                                        that identifier; if an SVG marker object,
                                        use that marker
text_attr               default={}      SVG attributes for the text labels
attribute=value pairs   keyword list    SVG attributes for the tick marks 

Standard tick specification:

    * True: same as -10 (below).
    * Positive number N: draw exactly N ticks, including the endpoints. To
      subdivide an axis into 10 equal-sized segments, ask for 11 ticks.
    * Negative number -N: draw at least N ticks. Ticks will be chosen with
      "natural" values, multiples of 2 or 5.
    * List of values: draw a tick mark at each value.
    * Dict of value, label pairs: draw a tick mark at each value, labeling
      it with the given string. This lets you say things like {3.14159: "pi"}.
    * False or None: no ticks.

Standard minitick specification:

    * True: draw miniticks with "natural" values, more closely spaced than
      the ticks.
    * Positive number N: draw exactly N miniticks, including the endpoints.
      To subdivide an axis into 100 equal-sized segments, ask for 101 miniticks.
    * Negative number -N: draw at least N miniticks.
    * List of values: draw a minitick mark at each value.
    * False or None: no miniticks. 

Standard tick label specification:

    * True: use the unumber function (described below)
    * Format string: standard format strings, e.g. "%5.2f" for 12.34
    * Python callable: function that converts numbers to strings
    * False or None: no labels

Definition at line 2320 of file svgfig.py.

Constructor & Destructor Documentation

def svgfig.Ticks.__init__	(	self,
		f,
		low,
		high,
		ticks = `-10`,
		miniticks = `True`,
		labels = `True`,
		logbase = `None`,
		arrow_start = `None`,
		arrow_end = `None`,
		text_attr = `{}`,
		attr
	)

Definition at line 2391 of file svgfig.py.

   def __init__(self, f, low, high, ticks=-10, miniticks=True, labels=True, logbase=None, arrow_start=None, arrow_end=None, text_attr={}, **attr):
     self.f = f
     self.low = low
     self.high = high
     self.ticks = ticks
     self.miniticks = miniticks
     self.labels = labels
     self.logbase = logbase
     self.arrow_start = arrow_start
     self.arrow_end = arrow_end
 
     self.attr = dict(self.defaults)
     self.attr.update(attr)
 
     self.text_attr = dict(self.text_defaults)
     self.text_attr.update(text_attr)
 

Member Function Documentation

def svgfig.Ticks.__repr__ ( self )

Definition at line 2388 of file svgfig.py.

References svgfig.SVG.attr, svgfig.Path.attr, svgfig.Curve.attr, svgfig.Poly.attr, svgfig.Text.attr, svgfig.TextGlobal.attr, svgfig.Dots.attr, svgfig.Line.attr, svgfig.LineGlobal.attr, svgfig.VLine.attr, svgfig.HLine.attr, svgfig.Rect.attr, svgfig.Ellipse.attr, svgfig.Ticks.attr, svgfig.Curve.f, svgfig.Line.f, svgfig.Rect.f, svgfig.Ellipse.f, svgfig.Ticks.f, svgfig.Curve.high, svgfig.Line.high, svgfig.Rect.high, svgfig.Ellipse.high, svgfig.Ticks.high, svgfig.Ticks.labels, svgfig.Curve.low, svgfig.Line.low, svgfig.Rect.low, svgfig.Ellipse.low, svgfig.Ticks.low, harvestTrackValidationPlots.str, and svgfig.Ticks.ticks.

Referenced by data_sources.json_file.__str__().

   def __repr__(self):
     return "<Ticks %s from %s to %s ticks=%s labels=%s %s>" % (self.f, self.low, self.high, str(self.ticks), str(self.labels), self.attr)
 

def svgfig.Ticks.compute_logminiticks	(	self,
		base
	)

Return optimal logarithmic miniticks, given a set of ticks.

Normally only used internally.

Definition at line 2769 of file svgfig.py.

References svgfig.Curve.high, svgfig.Line.high, svgfig.Rect.high, svgfig.Ellipse.high, svgfig.Ticks.high, createfilelist.int, svgfig.Curve.low, svgfig.Line.low, svgfig.Rect.low, svgfig.Ellipse.low, and svgfig.Ticks.low.

Referenced by svgfig.Ticks.interpret().

   def compute_logminiticks(self, base):
     """Return optimal logarithmic miniticks, given a set of ticks.
 
     Normally only used internally.
     """
     if self.low >= self.high: raise ValueError("low must be less than high")
 
     lowN = math.floor(math.log(self.low, base))
     highN = math.ceil(math.log(self.high, base))
     output = []
     num_ticks = 0
     for n in range(int(lowN), int(highN)+1):
       x = base**n
       if self.low <= x <= self.high: num_ticks += 1
       for m in range(2, int(math.ceil(base))):
         minix = m * x
         if self.low <= minix <= self.high: output.append(minix)
 
     if num_ticks <= 2: return []
     else: return output
 

def svgfig.Ticks.compute_logticks	(	self,
		base,
		N,
		format
	)

Return less than -N or exactly N optimal logarithmic ticks.

Normally only used internally.

Definition at line 2718 of file svgfig.py.

References funct.abs(), svgfig.Ticks.compute_ticks(), svgfig.Curve.high, svgfig.Line.high, svgfig.Rect.high, svgfig.Ellipse.high, svgfig.Ticks.high, createfilelist.int, svgfig.Curve.low, svgfig.Line.low, svgfig.Rect.low, svgfig.Ellipse.low, svgfig.Ticks.low, genParticles_cff.map, and min().

Referenced by svgfig.Ticks.interpret().

   def compute_logticks(self, base, N, format):
     """Return less than -N or exactly N optimal logarithmic ticks.
 
     Normally only used internally.
     """
     if self.low >= self.high: raise ValueError("low must be less than high")
     if N == 1: raise ValueError("N can be 0 or >1 to specify the exact number of ticks or negative to specify a maximum")
 
     eps = _epsilon * (self.high - self.low)
 
     if N >= 0:
       output = {}
       x = self.low
       for i in xrange(N):
         if format == unumber and abs(x) < eps: label = u"0"
         else: label = format(x)
         output[x] = label
         x += (self.high - self.low)/(N-1.)
       return output
 
     N = -N
 
     lowN = math.floor(math.log(self.low, base))
     highN = math.ceil(math.log(self.high, base))
     output = {}
     for n in range(int(lowN), int(highN)+1):
       x = base**n
       label = format(x)
       if self.low <= x <= self.high: output[x] = label
 
     for i in range(1, len(output)):
       keys = output.keys()
       keys.sort()
       keys = keys[::i]
       values = map(lambda k: output[k], keys)
       if len(values) <= N:
         for k in output.keys():
           if k not in keys:
             output[k] = ""
         break
 
     if len(output) <= 2:
       output2 = self.compute_ticks(N=-int(math.ceil(N/2.)), format=format)
       lowest = min(output2)
 
       for k in output:
         if k < lowest: output2[k] = output[k]
       output = output2
 
     return output
 

def svgfig.Ticks.compute_miniticks	(	self,
		original_ticks
	)

Return optimal linear miniticks, given a set of ticks.

Normally only used internally.

Definition at line 2689 of file svgfig.py.

References funct.abs(), svgfig.Curve.high, svgfig.Line.high, svgfig.Rect.high, svgfig.Ellipse.high, svgfig.Ticks.high, svgfig.Curve.low, svgfig.Line.low, svgfig.Rect.low, svgfig.Ellipse.low, svgfig.Ticks.low, min(), and svgfig.Ticks.ticks.

Referenced by svgfig.Ticks.interpret().

   def compute_miniticks(self, original_ticks):
     """Return optimal linear miniticks, given a set of ticks.
 
     Normally only used internally.
     """
     if len(original_ticks) < 2: original_ticks = ticks(self.low, self.high)
     original_ticks = original_ticks.keys()
     original_ticks.sort()
 
     if self.low > original_ticks[0] + _epsilon or self.high < original_ticks[-1] - _epsilon:
       raise ValueError("original_ticks {%g...%g} extend beyond [%g, %g]" % (original_ticks[0], original_ticks[-1], self.low, self.high))
 
     granularities = []
     for i in range(len(original_ticks)-1):
       granularities.append(original_ticks[i+1] - original_ticks[i])
     spacing = 10**(math.ceil(math.log10(min(granularities)) - 1))
 
     output = []
     x = original_ticks[0] - math.ceil(1.*(original_ticks[0] - self.low) / spacing) * spacing
 
     while x <= self.high:
       if x >= self.low:
         already_in_ticks = False
         for t in original_ticks:
           if abs(x-t) < _epsilon * (self.high - self.low): already_in_ticks = True
         if not already_in_ticks: output.append(x)
       x += spacing
     return output
 

def svgfig.Ticks.compute_ticks	(	self,
		N,
		format
	)

Return less than -N or exactly N optimal linear ticks.

Normally only used internally.

Definition at line 2601 of file svgfig.py.

References funct.abs(), svgfig.Curve.high, svgfig.Line.high, svgfig.Rect.high, svgfig.Ellipse.high, svgfig.Ticks.high, createfilelist.int, svgfig.Curve.low, svgfig.Line.low, svgfig.Rect.low, svgfig.Ellipse.low, svgfig.Ticks.low, and SiStripPI.max.

Referenced by svgfig.Ticks.compute_logticks(), and svgfig.Ticks.interpret().

   def compute_ticks(self, N, format):
     """Return less than -N or exactly N optimal linear ticks.
 
     Normally only used internally.
     """
     if self.low >= self.high: raise ValueError("low must be less than high")
     if N == 1: raise ValueError("N can be 0 or >1 to specify the exact number of ticks or negative to specify a maximum")
 
     eps = _epsilon * (self.high - self.low)
 
     if N >= 0:
       output = {}
       x = self.low
       for i in xrange(N):
         if format == unumber and abs(x) < eps: label = u"0"
         else: label = format(x)
         output[x] = label
         x += (self.high - self.low)/(N-1.)
       return output
 
     N = -N
 
     counter = 0
     granularity = 10**math.ceil(math.log10(max(abs(self.low), abs(self.high))))
     lowN = math.ceil(1.*self.low / granularity)
     highN = math.floor(1.*self.high / granularity)
 
     while (lowN > highN):
       countermod3 = counter % 3
       if countermod3 == 0: granularity *= 0.5
       elif countermod3 == 1: granularity *= 0.4
       else: granularity *= 0.5
       counter += 1
       lowN = math.ceil(1.*self.low / granularity)
       highN = math.floor(1.*self.high / granularity)
 
     last_granularity = granularity
     last_trial = None
 
     while True:
       trial = {}
       for n in range(int(lowN), int(highN)+1):
         x = n * granularity
         if format == unumber and abs(x) < eps: label = u"0"
         else: label = format(x)
         trial[x] = label
 
       if int(highN)+1 - int(lowN) >= N:
         if last_trial == None:
           v1, v2 = self.low, self.high
           return {v1: format(v1), v2: format(v2)}
         else:
           low_in_ticks, high_in_ticks = False, False
           for t in last_trial.keys():
             if 1.*abs(t - self.low)/last_granularity < _epsilon: low_in_ticks = True
             if 1.*abs(t - self.high)/last_granularity < _epsilon: high_in_ticks = True
 
           lowN = 1.*self.low / last_granularity
           highN = 1.*self.high / last_granularity
           if abs(lowN - round(lowN)) < _epsilon and not low_in_ticks:
             last_trial[self.low] = format(self.low)
           if abs(highN - round(highN)) < _epsilon and not high_in_ticks:
             last_trial[self.high] = format(self.high)
           return last_trial
 
       last_granularity = granularity
       last_trial = trial
 
       countermod3 = counter % 3
       if countermod3 == 0: granularity *= 0.5
       elif countermod3 == 1: granularity *= 0.4
       else: granularity *= 0.5
       counter += 1
       lowN = math.ceil(1.*self.low / granularity)
       highN = math.floor(1.*self.high / granularity)
 

def svgfig.Ticks.interpret ( self )

Evaluate and return optimal ticks and miniticks according to
the standard minitick specification.

Normally only used internally.

Definition at line 2507 of file svgfig.py.

References funct.abs(), svgfig.Ticks.compute_logminiticks(), svgfig.Ticks.compute_logticks(), svgfig.Ticks.compute_miniticks(), svgfig.Ticks.compute_ticks(), svgfig.Curve.high, svgfig.Line.high, svgfig.Rect.high, svgfig.Ellipse.high, svgfig.Ticks.high, svgfig.Ticks.labels, svgfig.Ticks.logbase, svgfig.Curve.low, svgfig.Line.low, svgfig.Rect.low, svgfig.Ellipse.low, svgfig.Ticks.low, svgfig.Ticks.miniticks, svgfig.Ticks.regular_miniticks(), and svgfig.Ticks.ticks.

   def interpret(self):
     """Evaluate and return optimal ticks and miniticks according to
     the standard minitick specification.
 
     Normally only used internally.
     """
 
     if self.labels == None or self.labels == False:
       format = lambda x: ""
 
     elif self.labels == True:
       format = unumber
 
     elif isinstance(self.labels, basestring):
       format = lambda x: (self.labels % x)
 
     elif callable(self.labels):
       format = self.labels
 
     else: raise TypeError("labels must be None/False, True, a format string, or a number->string function")
 
     # Now for the ticks
     ticks = self.ticks
 
     # Case 1: ticks is None/False
     if ticks == None or ticks == False: return {}, []
 
     # Case 2: ticks is the number of desired ticks
     elif isinstance(ticks, (int, long)):
       if ticks == True: ticks = -10
 
       if self.logbase == None:
         ticks = self.compute_ticks(ticks, format)
       else:
         ticks = self.compute_logticks(self.logbase, ticks, format)
 
       # Now for the miniticks
       if self.miniticks == True:
         if self.logbase == None:
           return ticks, self.compute_miniticks(ticks)
         else:
           return ticks, self.compute_logminiticks(self.logbase)
 
       elif isinstance(self.miniticks, (int, long)):
         return ticks, self.regular_miniticks(self.miniticks)
 
       elif getattr(self.miniticks, "__iter__", False):
         return ticks, self.miniticks
 
       elif self.miniticks == False or self.miniticks == None:
         return ticks, []
 
       else:
         raise TypeError("miniticks must be None/False, True, a number of desired miniticks, or a list of numbers")
         
     # Cases 3 & 4: ticks is iterable
     elif getattr(ticks, "__iter__", False):
 
       # Case 3: ticks is some kind of list
       if not isinstance(ticks, dict):
         output = {}
         eps = _epsilon * (self.high - self.low)
         for x in ticks:
           if format == unumber and abs(x) < eps:
             output[x] = u"0"
           else:
             output[x] = format(x)
         ticks = output
 
       # Case 4: ticks is a dict
       else: pass
 
       # Now for the miniticks
       if self.miniticks == True:
         if self.logbase == None:
           return ticks, self.compute_miniticks(ticks)
         else:
           return ticks, self.compute_logminiticks(self.logbase)
 
       elif isinstance(self.miniticks, (int, long)):
         return ticks, self.regular_miniticks(self.miniticks)
 
       elif getattr(self.miniticks, "__iter__", False):
         return ticks, self.miniticks
 
       elif self.miniticks == False or self.miniticks == None:
         return ticks, []
 
       else:
         raise TypeError("miniticks must be None/False, True, a number of desired miniticks, or a list of numbers")
         
     else:
       raise TypeError("ticks must be None/False, a number of desired ticks, a list of numbers, or a dictionary of explicit markers")
 

def svgfig.Ticks.orient_tickmark	(	self,
		t,
		trans = `None`
	)

Return the position, normalized local x vector, normalized
local y vector, and angle of a tick at position t.

Normally only used internally.

Definition at line 2408 of file svgfig.py.

References funct.abs(), svgfig.Curve.f, svgfig.Line.f, svgfig.Rect.f, svgfig.Ellipse.f, svgfig.Ticks.f, svgfig.Curve.high, svgfig.Line.high, svgfig.Rect.high, svgfig.Ellipse.high, svgfig.Ticks.high, svgfig.Curve.low, svgfig.Line.low, svgfig.Rect.low, svgfig.Ellipse.low, svgfig.Ticks.low, and svgfig.totrans().

   def orient_tickmark(self, t, trans=None):
     """Return the position, normalized local x vector, normalized
     local y vector, and angle of a tick at position t.
 
     Normally only used internally.
     """
     if isinstance(trans, basestring): trans = totrans(trans)
     if trans == None:
       f = self.f
     else:
       f = lambda t: trans(*self.f(t))
 
     eps = _epsilon * abs(self.high - self.low)
 
     X, Y = f(t)
     Xprime, Yprime = f(t + eps)
     xhatx, xhaty = (Xprime - X)/eps, (Yprime - Y)/eps
 
     norm = math.sqrt(xhatx**2 + xhaty**2)
     if norm != 0: xhatx, xhaty = xhatx/norm, xhaty/norm
     else: xhatx, xhaty = 1., 0.
 
     angle = math.atan2(xhaty, xhatx) + math.pi/2.
     yhatx, yhaty = math.cos(angle), math.sin(angle)
 
     return (X, Y), (xhatx, xhaty), (yhatx, yhaty), angle
 

def svgfig.Ticks.regular_miniticks	(	self,
		N
	)

Return exactly N linear ticks.

Normally only used internally.

Definition at line 2677 of file svgfig.py.

References svgfig.Curve.high, svgfig.Line.high, svgfig.Rect.high, svgfig.Ellipse.high, svgfig.Ticks.high, svgfig.Curve.low, svgfig.Line.low, svgfig.Rect.low, svgfig.Ellipse.low, and svgfig.Ticks.low.

Referenced by svgfig.Ticks.interpret().

   def regular_miniticks(self, N):
     """Return exactly N linear ticks.
 
     Normally only used internally.
     """
     output = []
     x = self.low
     for i in xrange(N):
       output.append(x)
       x += (self.high - self.low)/(N-1.)
     return output
 

def svgfig.Ticks.SVG	(	self,
		trans = `None`
	)

Apply the transformation "trans" and return an SVG object.

Definition at line 2435 of file svgfig.py.

References svgfig.totrans().

   def SVG(self, trans=None):
     """Apply the transformation "trans" and return an SVG object."""
     if isinstance(trans, basestring): trans = totrans(trans)
 
     self.last_ticks, self.last_miniticks = self.interpret()
     tickmarks = Path([], **self.attr)
     minitickmarks = Path([], **self.attr)
     output = SVG("g")
 
     if (self.arrow_start != False and self.arrow_start != None) or (self.arrow_end != False and self.arrow_end != None):
       defs = SVG("defs")
 
       if self.arrow_start != False and self.arrow_start != None:
         if isinstance(self.arrow_start, SVG):
           defs.append(self.arrow_start)
         elif isinstance(self.arrow_start, basestring):
           defs.append(make_marker(self.arrow_start, "arrow_start"))
         else:
           raise TypeError("arrow_start must be False/None or an id string for the new marker")
 
       if self.arrow_end != False and self.arrow_end != None:
         if isinstance(self.arrow_end, SVG):
           defs.append(self.arrow_end)
         elif isinstance(self.arrow_end, basestring):
           defs.append(make_marker(self.arrow_end, "arrow_end"))
         else:
           raise TypeError("arrow_end must be False/None or an id string for the new marker")
 
       output.append(defs)
 
     eps = _epsilon * (self.high - self.low)
 
     for t, label in self.last_ticks.items():
       (X, Y), (xhatx, xhaty), (yhatx, yhaty), angle = self.orient_tickmark(t, trans)
       
       if (not self.arrow_start or abs(t - self.low) > eps) and (not self.arrow_end or abs(t - self.high) > eps):
         tickmarks.d.append(("M", X - yhatx*self.tick_start, Y - yhaty*self.tick_start, True))
         tickmarks.d.append(("L", X - yhatx*self.tick_end, Y - yhaty*self.tick_end, True))
 
       angle = (angle - math.pi/2.)*180./math.pi + self.text_angle
 
       ########### a HACK! ############ (to be removed when Inkscape handles baselines)
       if _hacks["inkscape-text-vertical-shift"]:
         if self.text_start > 0:
           X += math.cos(angle*math.pi/180. + math.pi/2.) * 2.
           Y += math.sin(angle*math.pi/180. + math.pi/2.) * 2.
         else:
           X += math.cos(angle*math.pi/180. + math.pi/2.) * 2. * 2.5
           Y += math.sin(angle*math.pi/180. + math.pi/2.) * 2. * 2.5
       ########### end hack ###########
 
       if label != "":
         output.append(SVG("text", label, transform="translate(%g, %g) rotate(%g)" % \
                           (X - yhatx*self.text_start, Y - yhaty*self.text_start, angle), **self.text_attr))
 
     for t in self.last_miniticks:
       skip = False
       for tt in self.last_ticks.keys():
         if abs(t - tt) < eps:
           skip = True
           break
       if not skip:
         (X, Y), (xhatx, xhaty), (yhatx, yhaty), angle = self.orient_tickmark(t, trans)
 
       if (not self.arrow_start or abs(t - self.low) > eps) and (not self.arrow_end or abs(t - self.high) > eps):
         minitickmarks.d.append(("M", X - yhatx*self.minitick_start, Y - yhaty*self.minitick_start, True))
         minitickmarks.d.append(("L", X - yhatx*self.minitick_end, Y - yhaty*self.minitick_end, True))
 
     output.prepend(tickmarks.SVG(trans))
     output.prepend(minitickmarks.SVG(trans))
     return output
 